When Hannah Cairo was 17 years outdated, she disproved the Mizohata-Takeuchi conjecture, a long-standing guess within the discipline of harmonic evaluation about how waves behave on curved surfaces. The conjecture was posed within the Eighties, and mathematicians had been attempting to show it ever since. If the Mizohata-Takeuchi conjecture turned out to be true, it might illuminate many different vital questions within the discipline. However after hitting wall after wall attempting to show it, Cairo managed to give you a counterexample: a circumstance the place the waves don’t behave as predicted by the conjecture. Subsequently, the conjecture can’t be true.
Cairo obtained hooked on the issue after being assigned a less complicated model of the conjecture to show as a homework project for a category she was taking on the College of California, Berkeley. “It took me some time to persuade [course instructor] Ruixiang Zhang that my proposal was really appropriate,” she says. Now, beneath Zhang’s advisement, she has a paper on the preprint server arXiv.org and was invited to current her outcomes on the Worldwide Convention on Harmonic Evaluation and Partial Differential Equations in El Escorial, Spain.
On supporting science journalism
If you happen to’re having fun with this text, take into account supporting our award-winning journalism by subscribing. By buying a subscription you might be serving to to make sure the way forward for impactful tales concerning the discoveries and concepts shaping our world immediately.
Cairo says she loves speaking about her analysis and giving shows with colourful and descriptive slides (see examples under). When requested what she research, Cairo says, in brief, “factors, traces and waves.”
Born and raised within the Bahamas, Cairo moved to California on the age of 16, the place she started to take courses at U.C. Berkeley. Now, at 18 years outdated, she is on to a Ph.D. program on the College of Maryland to proceed her analysis in Fourier restriction principle. Cairo has confronted many difficulties in her journey, however she has discovered consolation and belonging within the discipline of arithmetic and within the work itself.
Scientific American spoke to Cairo about the best way harmonic evaluation is like dropping stones right into a nonetheless pond, her transgender id and the explanations she loves arithmetic.
[An edited transcript of the interview follows.]
Past “factors, traces, and waves,” how would you clarify your discipline of examine, harmonic evaluation?
Think about that you just’re at a pond, and it’s a really nonetheless pond, and also you drop a stone into it. You see these round waves spreading out.
If you happen to drop two stones within the pond, then you definitely would possibly discover this sample referred to as an interference sample: as a substitute of trying like circles, they overlap. You get excessive factors, low factors. And also you get these fascinating shapes [where they intersect]. What in the event you had been to make use of a complete bunch of ripples—then what would you get? In harmonic evaluation, you’ll be able to really show that in the event you drop your stones in the suitable place within the pond, you may get any form that you really want.

Slide from Hannah Cairo’s presentation on the Mizohata-Takeuchi Conjecture
My specialty is called Fourier restriction principle, which is the subdiscipline of harmonic evaluation that I work in, the place we ask what sort of objects can we construct if we’re solely allowed to make use of sure sorts of waves. What if we’re solely allowed to drop the stones in sure components of the pond? You received’t have the ability to get simply any object. The truth is, you’re solely going to have the ability to get a comparatively small household of objects. What the Mizohata-Takeuchi conjecture says is that the form of the objects that we get are concentrated alongside traces.
What does it imply to be “concentrated alongside traces”?
A technique to think about the form of objects is to ask: What’s curvature? There are a number of alternative ways you’ll be able to outline it. One doable manner is to take a skinny, lengthy rectangle and ask how a lot of your circle can lie on this skinny rectangle. What you’ll discover is that not very a lot of it could actually as a result of it bends away, proper? Alternatively, in the event you take one thing flat like the sting of a sq., then you may get a complete aspect of that sq. simply on one skinny tube. In order that signifies that the sq. will not be as “curved” as a circle.
For the Mizohata-Takeuchi conjecture, we are saying, take into account this object that we’re constructing out of those waves. And we need to say that not very a lot goes to lie on shapes that don’t comprise very many traces or skinny rectangles.
So how did you handle to disprove this conjecture?
I checked out these shapes, and one factor that I spotted is that the particular type of waves which might be used are concentrated alongside thick rectangles. That is really one thing that’s well-known. So you find yourself taking a look at these waves which might be targeting rectangles: You’re taking these waves, they usually intersect one another, they usually make these sure shapes, however right here [instead of circle waves] we use rectangle waves. So then we now have all of those rectangle waves assembly one another. What I spotted is that the form of the place they meet will not be fairly on the proper angle to agree with the route that these rectangles are pointing in. And so this led me to a fairly difficult development utilizing fractals to rearrange these rectangles.
The unique fractal development doesn’t really present up in your paper although. What was your remaining counterexample?
What I came upon is that in the event you prepare these waves by taking a high-dimensional hypercube and projecting it down into smaller-dimensional house after which taking solely these waves that lie in your area, then that is how one can decide the place to place them [to break the conjecture].
What first obtained you interested by math?
I’ve at all times been serious about math. I feel that, for me, arithmetic is an artwork. In my childhood, I used to be considerably lonely. Math was form of there as a buddy nearly. I feel that artwork can’t essentially be a buddy in each manner {that a} buddy may be, however I feel artwork is sort of a buddy. And so, for so long as I can bear in mind, I’ve at all times beloved arithmetic.
Inform me extra about how math was a buddy to you. I feel lots of people don’t consider math as very pleasant.
There’s an analogy that I prefer to make, which is to a different type of artwork: portray. And I feel that if one had been to take a category on paint, you could possibly memorize the dates and occasions at which numerous types of paint had been developed—and possibly even which paints had been utilized by which painters. After which you’ll be able to work out what processes you should utilize to find out what sort of paint it’s. I think about that is helpful in artwork historical past, however this isn’t artwork…. I shouldn’t say that. Possibly there’s an artwork to studying about paint. I’m not going to say that there isn’t as a result of I don’t examine paint. However I feel that math is a little bit bit like that—at school, individuals find out about [the mathematical version of] paint; they’re not studying about portray.
Arithmetic is reassuring to me as a result of it’s a manner of exploring—to discover concepts and to consider them and to construct extra concepts out of different concepts. What’s comforting about that’s that it’s unbiased of the world in some methods. If I’m having a tragic day, a cheerful day, if I transfer to Maryland (I did simply transfer to Maryland), arithmetic continues to be there, and it’s nonetheless the identical factor. It’s additionally simply one thing that may occupy my thoughts.
You’ve talked about to me that you just’re transgender. How has that affected your journey?
I feel that it’s most likely extra related in my journey as an individual than as a mathematician. Being trans has compelled me to see issues concerning the world that I possibly in any other case wouldn’t have seen. It’s made me see the world in a different way and made me see individuals in a different way and made me see myself in a different way.
Thankfully, within the math neighborhood, I feel that the majority mathematicians are nice with trans individuals. I feel that it was once extra vital [in my day to day] than it’s now. Nowadays it doesn’t actually make a lot of a distinction.
Why have you ever determined to go on the document now as being trans?
Trans visibility is essential. Folks have concepts about who trans persons are, and I feel that it’s finest to broaden that. Possibly I’m additionally hoping that individuals who assume that trans persons are “much less” than cisgender individuals would possibly discover themselves questioning that.
The opposite factor is that it’s good for trans individuals to know that they’re not alone. I feel that a part of what helps trans individuals understand that they’re trans is to know that there are extra choices for who you may be as a trans particular person. That’s essential to me.
Thanks a lot for sharing that. The place is your favourite place to do math?
If I’m attempting to be productive in writing one thing down, then I prefer to be at my desk, and I prefer to take heed to Bach. If I’m simply attempting to consider concepts, then my favourite place to try this is someplace the place I don’t have to concentrate to very a lot else. I may simply be sitting down someplace fascinated with stuff, or I may very well be going for a stroll exterior.
I additionally like to speak to different individuals about math, which is one other type of doing math. I actually like to present shows about arithmetic. I’ve these handwritten slides with all these colours and drawings. Fortunately, in harmonic evaluation, I can provide a presentation like this, after which everyone is so joyful, they usually inform me my slides are cute.
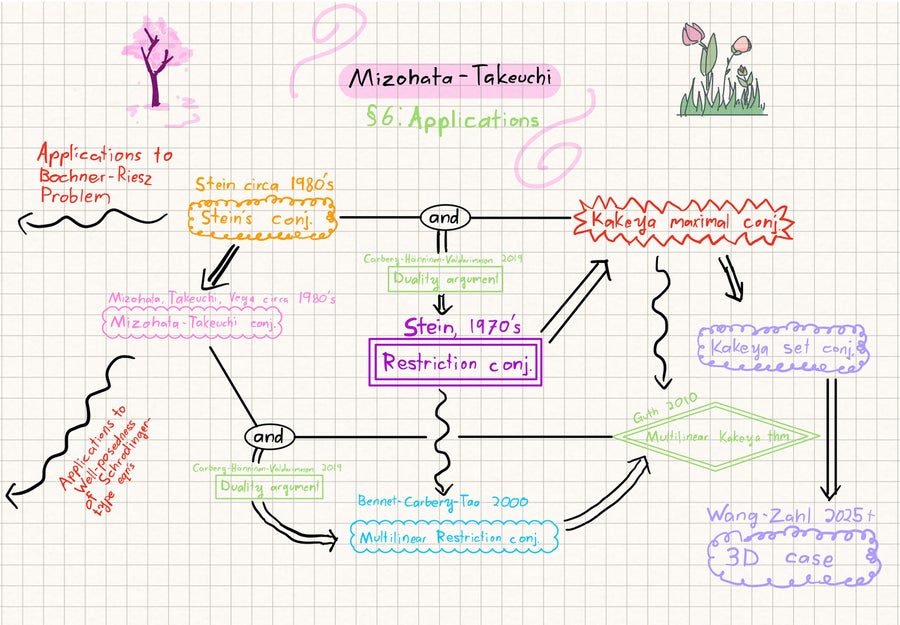
The ultimate slide from Cairo’s presentation on the Mizohata-Takeuchi Conjecture
What’s subsequent to your analysis?
I’m engaged on a analysis undertaking with my adviser on Mizohata-Takeuchi and adjoining stuff and a couple of form of completely different factor: the native Mizohata-Takeuchi conjecture.
The method of studying extra about this type of arithmetic is fairly thrilling—not only for me studying extra about what’s on the market however for the mathematics neighborhood as a complete to attempt to perceive these sorts of issues higher. [That’s] one thing that I’m enthusiastic about.

