This Block-Stacking Math Drawback Has a Preposterous Resolution You Have to See to Consider
In precept, this not possible math permits for a glue-free bridge of stacked blocks that may stretch throughout the Grand Canyon—and into infinity
Right here’s a mind-blowing experiment that you would be able to strive at residence: Collect some kids’s blocks and place them on a desk. Take one block and slowly push it over the desk’s edge, inch by inch, till it’s on the point of falling. In case you possess endurance and a gentle hand, it’s best to have the ability to stability it in order that precisely half of it hangs off the sting. Nudge it any farther, and gravity wins. Now take two blocks and begin over. Stacking one on high of the opposite, how far are you able to get the top of the highest block to poke over the desk’s edge?
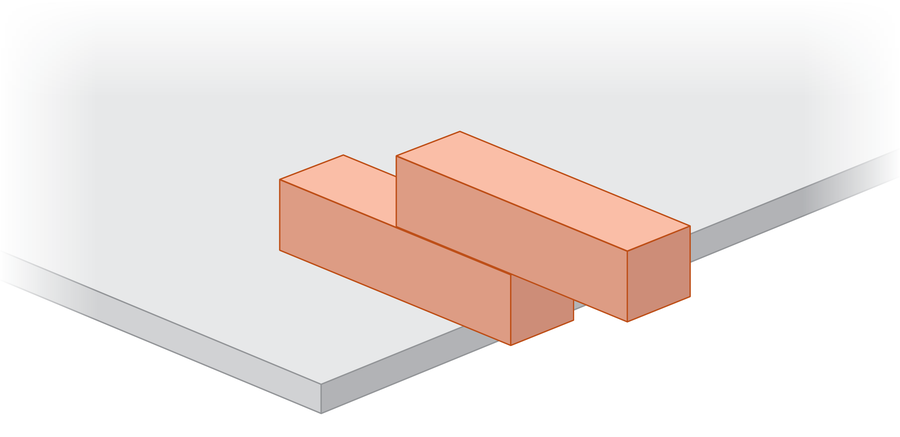
Maintain going. Stacking as many blocks as you may, what’s the farthest overhang you may obtain earlier than the entire construction topples? Is it attainable for the tower to increase a full block size past the lip of the desk? Does physics allow two block lengths? The beautiful reply is that the stacked bridge can stretch eternally. In precept, a freestanding stack of blocks can span the Grand Canyon, no glue required.
On supporting science journalism
In case you’re having fun with this text, think about supporting our award-winning journalism by subscribing. By buying a subscription you’re serving to to make sure the way forward for impactful tales in regards to the discoveries and concepts shaping our world in the present day.
Don’t click on “checkout” on an infinite pack of Jenga blocks simply but. Actual-world practicalities resembling irregular block shapes, air currents and the crushing weight of an countless edifice could hamper your engineering aspirations. Nonetheless, understanding why the overhang has no restrict in a super mathematical world is enlightening. The reason hinges on math’s harmonic sequence and the physics idea of middle of mass, two seemingly easy concepts with outsize energy. [For more fun, check out: How Tall Can You Build a Tower without It Toppling?]
Your instinct may let you know {that a} single block can dangle half of its mass past the desk’s edge earlier than tipping. However why is that so? Each object has a middle of mass—a single level at which we will think about your entire object’s weight to be concentrated after we’re excited about stability. So long as the middle of mass sits above the desk, the item stays put. The second that middle of mass passes over an edge, nevertheless, gravity will pull the entire thing over. Within the case of a spoon, an merchandise with irregular weight distribution, we will dangle greater than half of the utensil’s deal with over an edge earlier than it suggestions as a result of the middle of mass lies nearer to its head, the place extra of the load resides. For our stacked bridge, we assume that our blocks are all equivalent, with a uniform density (that’s, they’re not denser in some elements than others), so each’s middle of mass sits on the center level.
Once we add extra blocks, we should account for the middle of mass of your entire tower. Contemplate the case of two blocks. We all know the highest block can lengthen half of its mass past the one beneath it. However after doing that, how far can we push out the underside block?
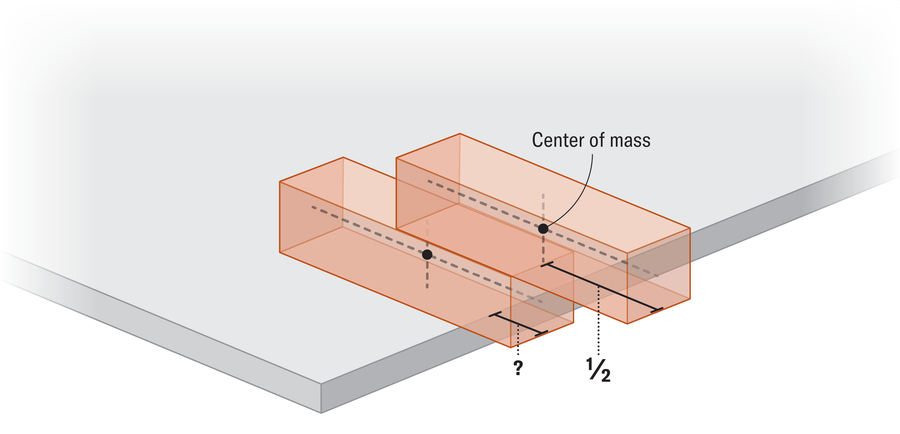
For simplicity, let’s say every block has a size of 1 and a mass of 1. You’ll discover the underside block can poke out solely 1 / 4 of the best way (in contrast with having half its size over the sting when it was alone). At that time, the middle of mass of the highest block and the middle of mass of the underside block are equidistant from the sting of the desk (the highest block’s middle of mass sits one quarter to the precise of the sting, and the underside block’s middle of mass sits one quarter to the left of the sting). So the mixed middle of mass of the two-block system rests completely balanced above the sting of the desk.
A sample emerges as we proceed so as to add blocks to the construction. The highest block extends 1⁄2 past the one beneath it, the second block extends 1⁄4 past the block beneath it, the third extends 1⁄6, the fourth extends 1⁄8, then subsequent blocks lengthen 1⁄10, 1⁄12, and so forth. To see why, let’s take a look at one other instance. Suppose we have now a steady tower that incorporates 5 blocks, and we need to add a sixth block beneath it after which slide the entire construction out so far as we will. It’s useful to conceptualize this image as solely two blocks: one with a mass of 5 atop a single block with a mass of 1. We’ll first scoot the heavy block so far as it would go in order that its middle of mass sits proper above the underside block’s edge. We are able to then push the underside block precisely 1⁄12 of a unit past the desk’s edge. How do we all know that?
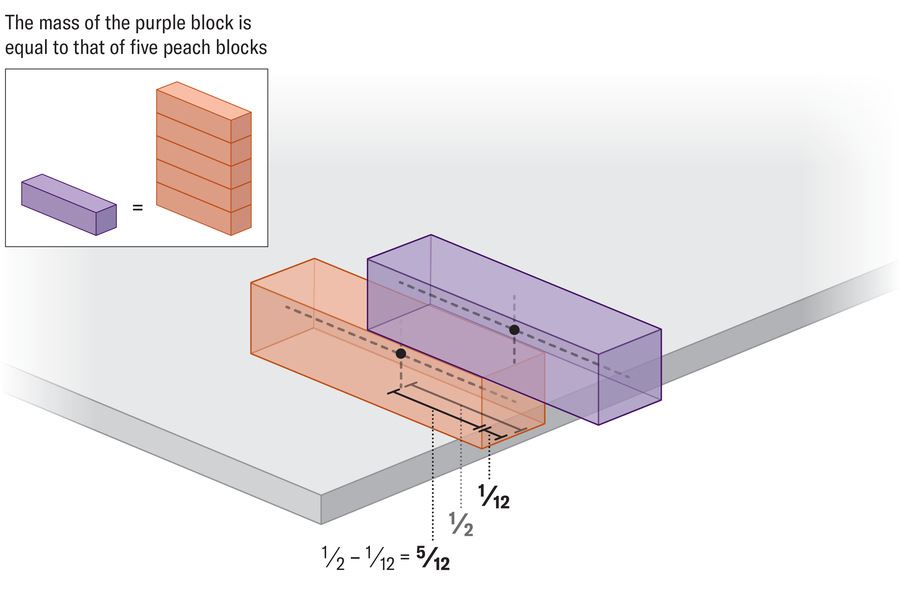
Once more, the reply comes right down to balancing out the facilities of mass of the 2 blocks, solely this time, as a result of the underside block is 5 occasions lighter, its middle of mass should find yourself 5 occasions farther on the tabletop to counteract the load of the heavier block. This is named the regulation of the lever—take into consideration how a ebook feels heavier in your palm the farther you progress it away out of your physique, so a paperback in a totally prolonged arm may really feel equal to a textbook held near your torso. The gap between the middle of mass of the highest block and the desk’s edge is 1⁄12, and the space for the underside block is 1⁄2 – 1⁄12 = 5⁄12, or 5 occasions extra. The same calculation reveals the proper overhang at each stage of the tower.
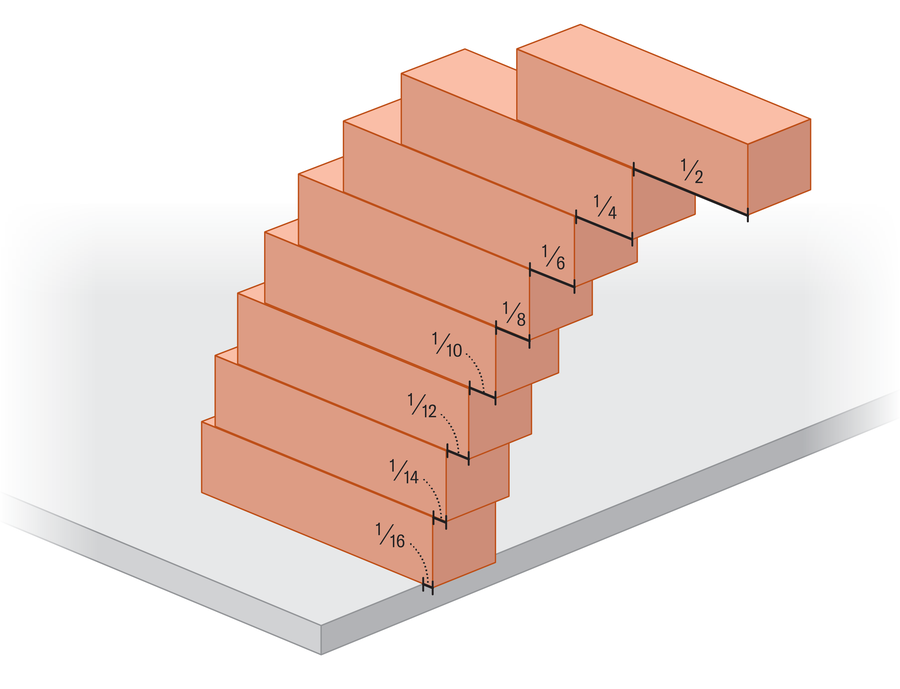
Answering our opening query (how far out can the tower lengthen?) quantities to including up all of those successive overhangs. When you have 10 blocks, they’ll lengthen to 1⁄2 + 1⁄4 + 1⁄6 + 1⁄8 + 1⁄10 + 1⁄12 + 1⁄14 + 1⁄16 + 1⁄18 + 1⁄20, which provides as much as about 1.464 block lengths past the sting. However what’s the restrict to how far we will stack blocks? For that, we should add infinitely many of those shrinking phrases. The ensuing sample bears a putting resemblance to probably the most well-known infinite sums in math, the harmonic sequence, which takes the reciprocal of each counting quantity (that’s, 1 divided by each constructive integer) and sums all of them:
1 + 1⁄2 + 1⁄3 + 1⁄4 + 1⁄5 + …, and so forth eternally.
In case you look intently, you may discover that the overhangs from the block-stacking drawback are precisely half of every of those phrases: 1⁄2 + 1⁄4 + 1⁄6 + 1⁄8 + 1⁄10 + …
Calculus, the department of math that digs into how issues change, teaches us that even when including up infinitely many shrinking phrases, generally the sum converges on a finite worth and generally it diverges to infinity. The whole of the harmonic sequence grows extremely slowly. The primary 100,000 phrases add as much as about 12.1 whereas the primary million phrases solely equal round 14.4. Nonetheless, at a relentless snail’s tempo, the harmonic sequence grows eternally.
Every particular person overhang within the block-stacking drawback equals half of a time period within the harmonic sequence. As a result of half of infinity remains to be infinity, the tower’s potential overhang additionally has no certain.
After all, translating pure math into observe at all times comes with hurdles, however the block-stacking drawback affords an amusing dexterity problem. With solely 4 blocks, it’s best to have the ability to lengthen the highest one a full block size previous the sting (1⁄2 + 1⁄4 + 1⁄6 + 1⁄8 = ~1.042). To meet my journalistic due diligence, I attempted this at residence with enjoying playing cards on my espresso desk. After a couple of minutes of affected person tinkering, I managed to stability the highest card simply past the sting, with it hanging fully off the desk, and I felt like a magician.
Two full block lengths past any floor would require 31 items. Meanwhile100 million items wouldn’t even get you a full 10 block lengths of overhang as a result of the sum of the primary 100 million phrases within the harmonic sequence all divided by 2 equals about 9.5. So it would take some grit to span the Grand Canyon. At large scales, physics kicks in to topple mathematicians’ enjoyable. However in idealized situations the place middle of mass and the harmonic sequence alone rule the roost, the probabilities are actually countless.

