Two Möbius Strips Mix to Create a Weird Object That Solely Exists in 4D
In geometry, there are surfaces that do with out an inside or exterior—and a few want not less than 4 dimensions to exist

LAGUNA DESIGN/SCIENCE PHOTO LIBRARY/Getty Pictures
Visually, the “Klein bottle” doesn’t appear all that spectacular. On first look it appears like a classy Japandi-style vase. And but it has fascinated mathematicians for greater than 140 years.
To grasp why, we now have to journey far again to the traditional Roman Empire, the place the primary traces of a considerably easier geometric form may be discovered: the Möbius strip. This enigmatic form is extremely simple to make: Take a protracted strip of paper and convey each ends collectively. However earlier than you glue the ends to one another, rotate one by 180 levels. The result’s a twisted band.
From a mathematical perspective, Möbius strips are fascinating as a result of they’ve just one floor and one edge. In contrast to a cylindrical object (comparable to one created by gluing collectively the ends of a strip that hasn’t been twisted), there isn’t any inside or exterior. For physicists, these twisted shapes make for wonderful factors of comparability when considering the properties of subatomic particles, such because the spin of the electron, which should be rotated by 720 levels to get again to its begin. And in factories, Möbius strips have been used as conveyor belts as a result of they put on out considerably extra slowly than untwisted belts, for which just one facet is pressured.
On supporting science journalism
In the event you’re having fun with this text, contemplate supporting our award-winning journalism by subscribing. By buying a subscription you might be serving to to make sure the way forward for impactful tales concerning the discoveries and concepts shaping our world immediately.
You may contact each level of a Möbius strip by working your finger alongside the form’s floor with out lifting it. Mathematicians discuss with this as a “nonorientable” floor. In the event you take pleasure in hands-on experiments, I extremely advocate attempting to minimize a Möbius strip lengthwise in several methods—the outcomes are astonishing.
The German mathematician Felix Klein was additionally fascinated by the probabilities of those unusual surfaces. He reasoned that should you glued two abnormal strips collectively alongside their respective edges, you could possibly get a wider strip—that’s, one edge of every strip would disappear. However a Möbius strip solely has a single edge. So what occurs should you glue two Möbius strips collectively? On this case, a floor with out a border outcomes. This unusual creation is the Klein bottle, a floor that, like a Möbius strip, has neither an inside nor an out of doors.
Combining Möbius Strips
Now, should you’re on the brink of begin taping collectively strips of paper to place this concept into motion, I’m afraid I’ve to disappoint you. A real Klein bottle can solely be created in 4 spatial dimensions. Sure, there are bottles impressed by the Klein bottle that exist in three dimensions, however they’re technically simply artifacts of the true Klein bottle in 4 dimensions. That’s as a result of, once you embed this determine in 3D house, the bottle will invariably intersect itself, an impediment that doesn’t come up once you form it in 4D house.
That mentioned, we will not less than attempt to visualize the Klein bottle. Think about gluing the correct and left edges of a chunk of paper collectively, forming an abnormal cylinder. You then glue the highest and backside edges collectively. However first, as with the Möbius strip, you twist them by 180 levels.
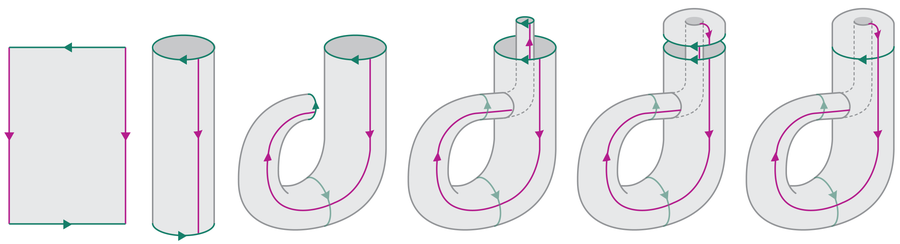
Just like the Möbius strip, the Klein bottle additionally possesses fascinating mathematical properties. Amongst different issues, it represents the one exception to the Ringel-Youngs theorem, which offers with the coloring of objects. For instance, if you wish to draw a map and coloration the person nations with out neighboring nations having the identical coloration, you solely want 4 totally different colours—no matter how the nations are organized.
Extra typically, the Ringel-Youngs four-color theorem states the utmost variety of colours wanted to paint nations on surfaces of various shapes. Because it seems, this will depend on the variety of holes within the surfaces. For instance, I would resolve to create a map for a doughnut-shaped planet. What’s the most variety of colours I would wish in that case? As a result of the planet has one gap, it follows from the theory that, at most, seven colours will suffice.
The Ringel-Youngs theorem applies to all surfaces besides the Klein bottle. In keeping with the theory, the Klein bottle ought to solely be colorable with a most of seven colours; because it seems, nonetheless, six colours are all the time ample for the small bottle.
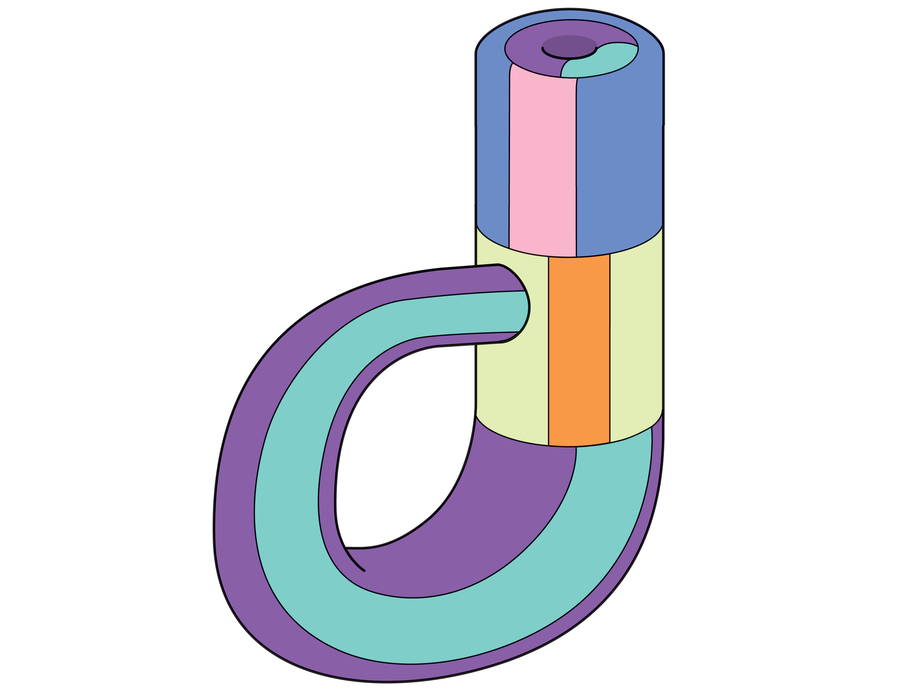
Due to such distinctive properties—and its nonorientability—the Klein bottle is considered one of a number of widespread and mind-bending objects amongst mathematicians. It additionally seems in physics, the place it might probably assist describe advanced quantum states, a lot because the Möbius strip illustrates spin states.
When you have any nerdy buddies, the 3D Klein bottle—although not fairly the actual deal—could possibly be an amazing Christmas current. You may even use it as a vase or wine decanter.
This text initially appeared in Spektrum der Wissenschaft and was reproduced with permission.
It’s Time to Stand Up for Science
In the event you loved this text, I’d prefer to ask to your help. Scientific American has served as an advocate for science and business for 180 years, and proper now will be the most crucial second in that two-century historical past.
I’ve been a Scientific American subscriber since I used to be 12 years outdated, and it helped form the way in which I have a look at the world. SciAm all the time educates and delights me, and conjures up a way of awe for our huge, lovely universe. I hope it does that for you, too.
In the event you subscribe to Scientific American, you assist be sure that our protection is centered on significant analysis and discovery; that we now have the assets to report on the choices that threaten labs throughout the U.S.; and that we help each budding and dealing scientists at a time when the worth of science itself too usually goes unrecognized.
In return, you get important information, charming podcasts, good infographics, can’t-miss newsletters, must-watch movies, difficult video games, and the science world’s finest writing and reporting. You may even reward somebody a subscription.
There has by no means been a extra essential time for us to face up and present why science issues. I hope you’ll help us in that mission.

